20 May 2019 Cálculo de rutas óptimas entre puntos de interés

Toni Hernández

Como ya vimos en este post anterior el cálculo de rutas óptimas requiere, obligatoriamente, una estructura de datos conocida como grafo. A modo de resumen un grafo define todas las conexiones posibles dentro de un espacio cartográfico mediante la definición de vértices y arcos, donde los vértices son los puntos de conexión entre arcos distintos.

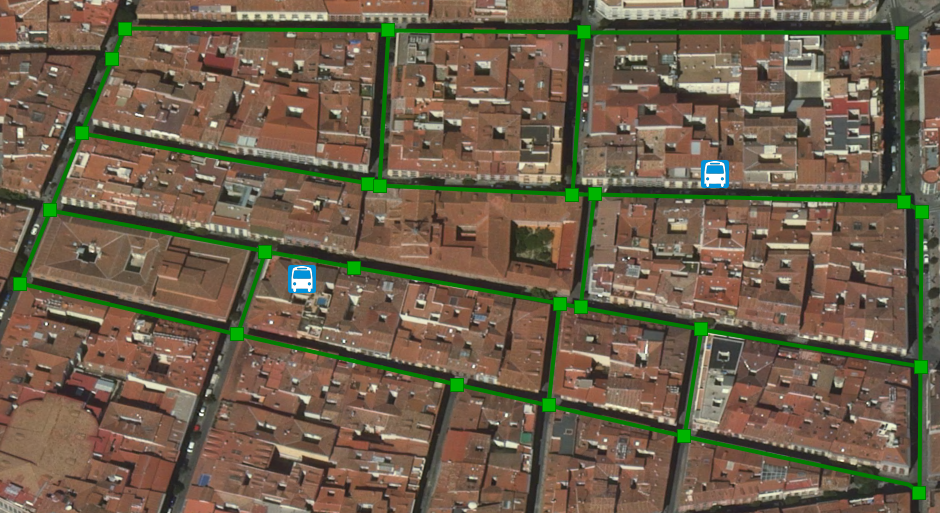
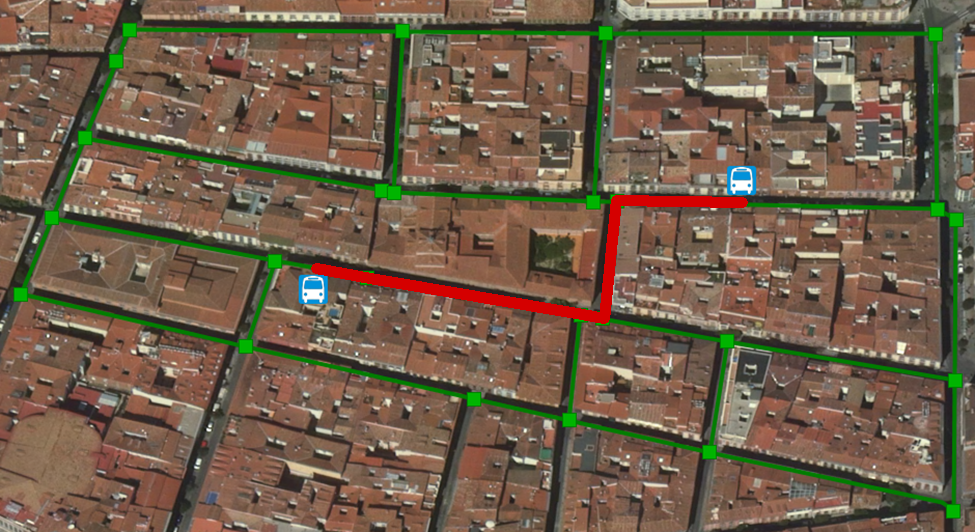
En la siguiente imagen, los cuadrados representan los nodos y las líneas los arcos.

La ruta óptima se define por ser la ruta de menor coste (en tiempo, distancia, etc). El coste de cada ruta se obtiene sumando los costes de los arcos por los que transita dicha ruta.

La principal limitación de estos algoritmos es que solo permiten el cálculo de rutas óptimas comprendidas entre dos nodos, pero, ¿qué pasa si queremos desplazarnos entre dos paradas de autobús situadas en algún lugar fuera de nuestro grafo? O, el ejemplo más habitual, ¿cómo podemos obtener la ruta entre dos direcciones postales localizadas en algún punto en medio de dos arcos?

Para dar respuesta a este tipo de peticiones PostGIS ofrece la función pgr_WithPoints(). En el siguiente apartado vamos a introducir esta función con más detalle y vamos a calcular la ruta óptima (más corta) que existe entre dos paradas de autobús. Como se aprecia en la imagen anterior, ninguna de las dos paradas de autobús coinciden con los nodos que componen el grafo.

Para seguir este ejemplo podéis uilizar las sentencias SQL que encontraréis en el siguiente archivo: dataset.zip.

pgr_WithPoints()

Antes de seguir con nuestro ejemplo práctico, vamos a ver cuales son los cuatro parámetros que acepta esta función:

 pgr_WithPoints(edges_sql, points_sql, start_vid, end_vid)

Donde:

EDGES_SQL: Representan los arcos del grafo con sus atributos.
POINTS_SQL: Puntos de interés ajenos al grafo con sus atributos.
START_VID: Nodo del grafo o punto de interés utilizado como origen.
END_VID: Nodo del grafo o punto de interés utilizado como destino.

Esta función, en su variante más sencilla, permite el cálculo de rutas óptimas indicando, como puntos de origen y destino, tanto vértices del grafo como puntos de interés ajenos al grafo, como por ejemplo, las paradas de autobús de nuestro ejemplo.

Tabla puntos De Interés

Además de las tablas necesarias para definir un grafo (arcos y nodos), en esta ocasión vamos a necesitar una tabla adicional donde almacenar los puntos de interés que son ajenos al grafo.

Esta tabla puede contener, tanto los puntos de interés de nuestra ciudad (bares, restaurantes, paradas de autobús, etc), como los números de los portales de un callejero. En este segundo caso, sería posible el cálculo de rutas óptimas entre direcciones postales concretas.

Estos son los atributos que vamos a necesitar en nuestra tabla puntosDeInteres.

– id: Atributo identificativo de cada punto de interés. Clave primaria.
– x: Atributo numérico de tipo float. Define la longitud de los puntos de interés
– y: Atributo numérico de tipo float. Define la latitud de los puntos de interés
– edge_id: Valor numérico. Indica el arco del grafo sobre el que se asigna un punto de interés.
– fraction: Valor numérico comprendido entre 0 y 1. Indica la posición del punto de interés dentro del arco correspondiente. Un valor igual a cero indica que el punto de interés está justo al inicio del arco, un valor 0.5 indica que está justo en medio del arco, etc.
– the_geom: Geometría del punto de interés.
– closestPoint: Geometría del punto de interés proyectado sobre el arco asignado.

La imagen anterior muestra, en primer lugar, la posición original de la parada de autobús (atributo the_geom). En segundo lugar, un círculo rojo que representa la posición de la parada proyectada sobre el arco más cercano (atributo closestPoint) y, finalmente, la fracción del punto proyectado sobre el arco correspondiente (atributo fraction). Esta fracción solo puede alcanzar valores dentro del rango [0 – 1], donde 0 se corresponde con el punto inicial del arco, 0.5 con el punto medio, 1 con el punto final, etc.

Caso de uso

Con esta estructura de tablas (arcos, nodos y puntos de interés) y estos datos debidamente insertados en todas sus columnas, ahora sí, podemos ejecutar la función pgr_WithPoints() del siguiente modo.

SELECT * FROM pgr_withPoints(
'SELECT id, source, target, st_length(the_geom) as cost FROM arcos ORDER BY id',
'SELECT pid, edge_id, fraction FROM puntosDeInteres',
-2,
-1
)

Los puntos de origen (-2) y final (-1) se refieren a las dos paradas de autobús de la tabla puntosDeInteres y deben indicarse como valores negativos. En caso contrario serían considerados nodos del propio grafo.

La consulta anterior retorna, en formato de tabla, la ruta óptima entre las dos paradas tal y como se muestra en la siguiente imagen.

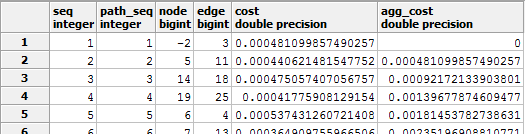
Donde cada fila indica un arco (o fracción de arco) por el que transita la ruta óptima obtenida. La columna cost se corresponde con la longitud de cada arco ya que estamos calculando la ruta más corta (coste = longitud). Este coste se calcula en función de si la ruta transita por todo el arco o si transita solo por una fracción de dicho arco.

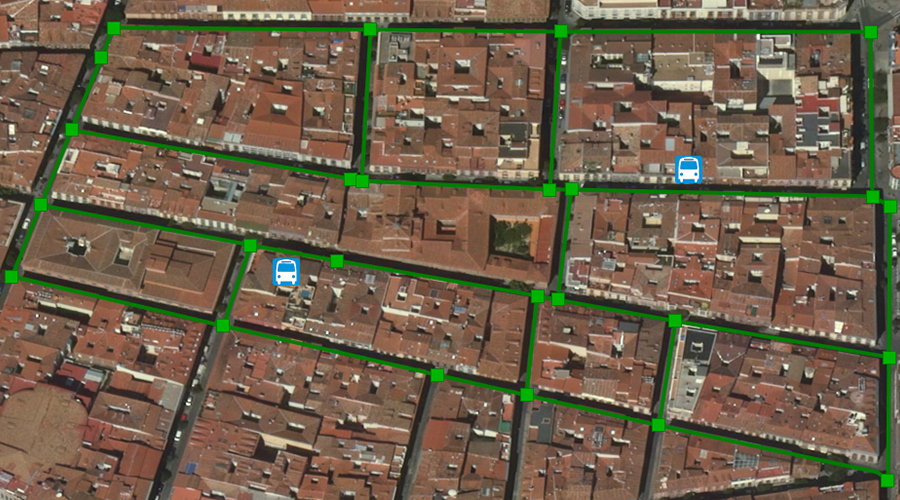
A partir del resultado anterior, podemos extender nuestra consulta para obtener la geometría de la ruta óptima obtenida tal y como aparece en la siguiente imagen. Este y otros comandos están disponibles en el archivo dataset.zip.

Ruta óptima obtenida